
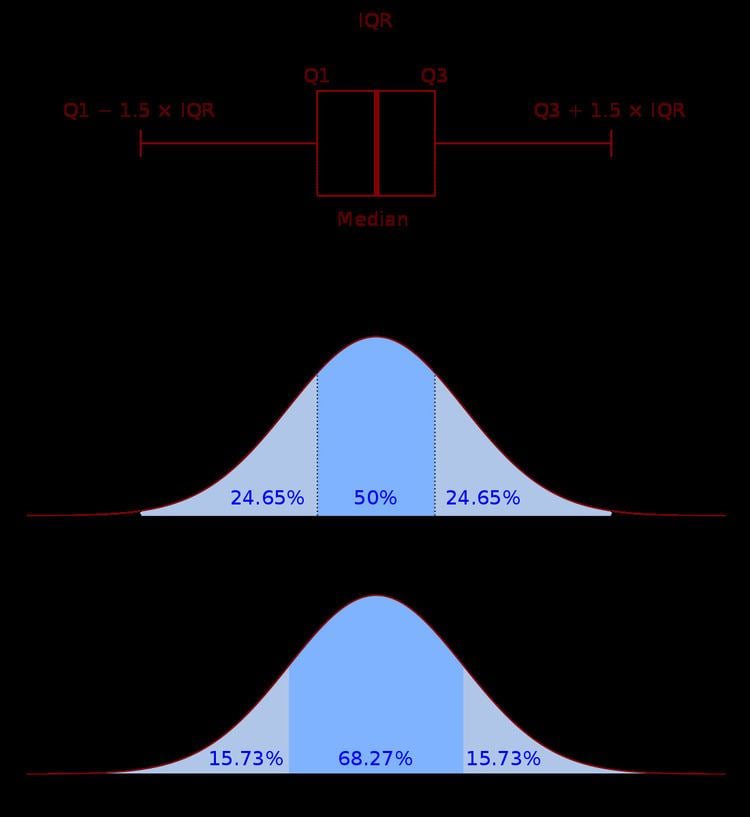
However, the IQR is a great option for skewed distributions. Using the standard deviation of a normal distribution, you can calculate the proportion of observations that fall within a certain distance of the mean.
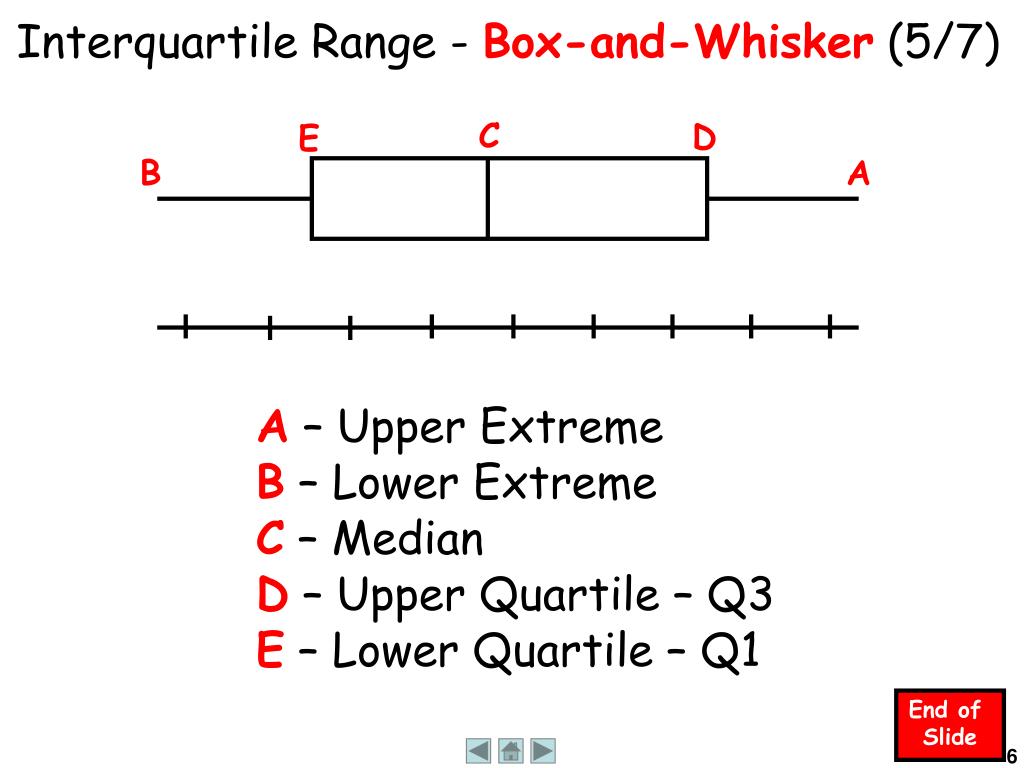
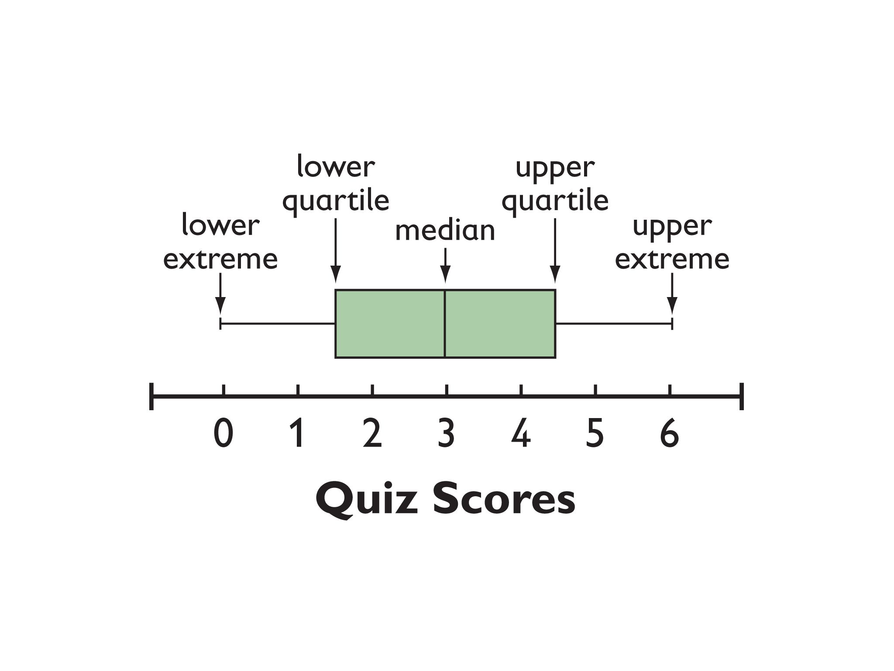
Interquartile range is also excellent for skewed distributions, like the median. Because they don’t rely on every number, outliers have little effect on either statistic. Measures like the interquartile range and the median are more robust than the more often used mean and standard deviation. The distribution of your data is better understood when you combine the two methods. Use the IQR with a central tendency measurement like the median to get a sense of your data’s distribution. In the graph below, the IQR is the red rectangle that includes Q2 and Q3 (not labeled).īecause extreme values and outliers have a less impact on the interquartile range, statisticians choose to use it instead of the complete data range when assessing variability. There are 50 percent of data points that are above Q1 and lower than Q4. The interquartile range (IQR) is the portion of the data that falls between the upper and lower quartiles of the distribution. The upper quartile (Q4) includes the highest values. The dataset’s smallest quarter is represented by the dataset’s lowest quartile (Q1). Quartiles are statistical divisions that are labelled from the lowest to the highest as Q1, Q2, Q3, and Q4. Interquartile Range Definitionĭivide your data into quarters to see the interquartile range.
A data science online course will give you more insights into the topic. The interquartile range, often known as IQR, is one of the numerous variables that are capable of being quantified in structure. The interquartile range, often known as IQR, may be used to analyse variability, present it in boxplots in order to investigate distributional characteristics, identify data outliers, and determine whether or not your data are regularly distributed. Read this article to get an understanding of what the interquartile range is and how it might be used.

As a consequence of this, lower values suggest that the values in the centre are grouped together more tightly. When compared to lower numbers, larger ones indicate a greater degree of dispersion in the central area of your data. The interquartile range, often known as the IQR, is a helpful tool for measuring the amount of variation that exists among a set of data points. This is the range of values for the portion of your data collection that falls in the centre. Note: We use 0.25 for Q1 since it's the value at the 25th percentile of the data.Ĥ) Find the difference between the results in steps 2 and 3.The interquartile range is a measure of the spread of your data that falls between the two extremes of the distribution (IQR). There is no button for quantiles, so you need to type the command using the a-z keyboard.ģ) Find Q1 by using the syntax: quantile (A, 0.25) Notes: We use 0.75 for Q3 since it's the value at the 75th percentile of the data. To find the IQR with the app, use the following steps:Ģ) Find Q3 by using the syntax: quantile(A, 0.75) Round 1.75 off to 2, so Q1 is the 2nd value in the set which is 5įinding the IQR is simple with small data sets, but it is easier to use the app for larger ones. Round 5.25 off to 5, so Q3 is the 5th value in the set which is 9. where k is the quartile and n is the number of values (observations).Ī) If c is a whole number, the quartile value is the average of the values at c and c + 1.ī) If c is not a whole number, the quartile value is the value at the integer when c is rounded off.įind the IQR of the data set: 12, 4, 5, 6, 9, 10, 8.ġ) Order the data set from lowest to highest. Finding the IQR requires the following steps:ġ) Arrange the data sets from least to highest.Ģ) Find the values of the 3rd quartile (Q3) and the 1st quartile (Q1) values by using the locator's formula: c = k(n)/4.


 0 kommentar(er)
0 kommentar(er)
